異名同音程/音程の転回/複音程【度数をもっと詳しく】

前回勉強した度数の基本を踏まえて、今回は「異名同音程」「音程の転回」「複音程」についてまとめてみました。
前回の記事はこちら。
スポンサーリンク
度数についてもう少し詳しく
「度数」って何?という方は前回の記事も併せてお読みください。
度数の基本:「度数」とは音程の数え方です
異名同音程
以下の図をご覧ください。

*同じ音程では??*
Cから見た増2度(長2度がさらに半音広がった音程)と短3度です。ちょっとピアノの鍵盤を思い浮かべてみてくださいね。レのシャープとミのフラット…そう、同じ音程なんです。
こういった度数は違うのに同じ音程のことを異名同音程と呼びます。
【※ややこしい話ですが、異名同音程はあくまで平均率(1オクターブを均等に十二等分するという調律法)に基づいたもので、本来の純正音程では違う音程になるそうです。】
異名同音程は主にその曲の調によって使い分けられます。
音程の転回
音程を構成する2音の内、1音のオクターブを上下させることにより、音名はそのままにその関係を入れ替えることができます。
これを音程の転回と呼びます。
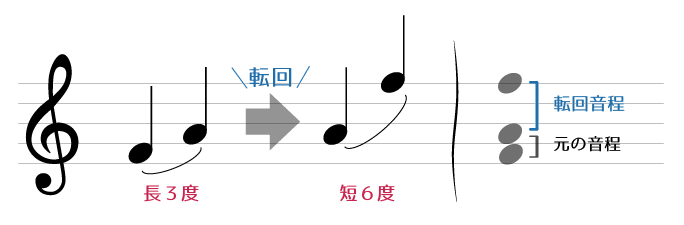
*Fの音をオクターブ上に転回*
図はFとA(長3度)の、Fのオクターブを1つ上げて(音程の転回をして)音程が短6度に変化したものです。この時、転回後の音程を「転回音程」と呼びます。
図からもわかる通り、音程の転回には以下のような特徴があります。
1.度数が変換される
小さな音程は大きく、大きな音程は小さい音程に変換されます。
・1度 ⇔ 8度
・2度 ⇔ 7度
・3度 ⇔ 6度
・4度 ⇔ 5度
※変換前の度数をn、変換後の度数をiと置くと、常に【n + i = 9】が成り立ちます。
2.度数の種類が変換される
先ほどと同じ理屈で、小さい度数の種類は大きい度数の種類に、大きい度数の種類は小さい度数の種類に変換されます。
・短 ⇔ 長
・減 ⇔ 増
・重減 ⇔ 重増
・完全 ⇔ 完全
※完全系については変換しても種類が変わりません。このことから、完全4度と完全5度は相互に変換できるということがわかります。さすが完全系。
単音程と複音程
完全8度までの音程(1オクターブ以内)の音程を単音程、それ以上の音程を複音程と呼びます。※増8度と重増8度も複音程に分類されます。
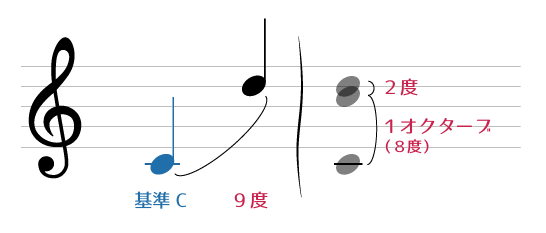
*複音程の例(Cから見た9度の音程)*
8度と2度を単純に足すと10度になってしまうので少し混乱しますが、1、2、3、4…と普通に数えると9度ですよね。自分自身の音を1度と数えることからこのような差異が生まれるわけです。
図の例は1オクターブ + 長2度なので正確には長9度になります。
また、そのまま「1オクターブと長2度」と呼ぶことも出来ますが、ギターのテンションコードなどを理解する上では前者の方がわかりやすいかもしれません。
以上、今回は度数の発展として【異名同音程/音程の転回/複音程】について勉強しました。
